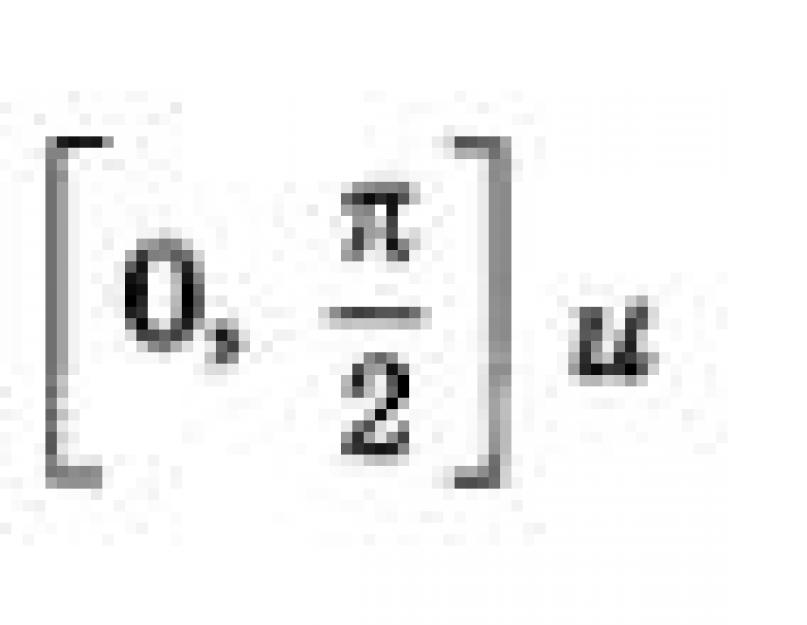>>Математика: Функции у = sin х, у = cos x, их свойства и графики

Функции у = sin х, у = cos x, их свойства и графики

В этом параграфе мы обсудим некоторые свойства функций у = sin х,у = соs х и построим их графики.

1. Функция у = sin X.

Выше, в § 20, мы сформулировали правило, позволяющее каждому числу t поставить в соответствие число cos t, т.е. охарактеризовали функцию y = sin t. Отметим некоторые ее свойства.

Свойства функции u = sin t.

Область определения - множество К действительных чисел.
Это следует из того, что любому числу 2 соответствует на числовой окружности точка М(1), которая имеет вполне определенную ординату; эта ордината и есть cos t.

u = sin t - нечетная функция.

Это следует из того, что, как было доказано в § 19, для любого t выполняется равенство
Значит, график функции и = sin t, как график любой нечетной функции, симметричен относительно начала координат в прямоугольной системе координат tOи.

Функция u = sin t возрастает на отрезке
Это следует из того, что при движении точки по первой четверти числовой окружности ордината постепенно увеличивается (от 0 до 1 - см. рис. 115), а при движении точки по второй четверти числовой окружности ордината постепенно уменьшается (от 1 до 0 - см. рис. 116).

Функция u = sin t ограничена и снизу, и сверху. Это следует из того, что, как мы видели в § 19, для любого t справедливо неравенство

(этого значения функция достигает в любои точке вида (этого значения функция достигает в любой точке вида
Воспользовавшись полученными свойствами, построим график интересующей нас функции. Но (внимание!) вместо u - sin t будем писать у = sin x (ведь нам привычнее запись у = f(х), а не u = f(t)). Значит, и строить график будем в привычной системе координат хОу (а не tOy).

Составим таблицу значений функции у - sin х:

Замечание.

Приведем одну из версий происхождения термина «синус». По-латыни sinus означает изгиб (тетива лука).

Построенный график в какой-то степени оправдывает эту терминологию.

Линию, служащую графиком функции у = sin х, называют синусоидой. Ту часть синусоиды, которая изображена на рис. 118 или 119, называют волной синусоиды, а ту часть синусоиды, которая изображена на рис. 117, называют полуволной или аркой синусоиды.

2. Функция у = соs х.

Изучение функции у = соs х можно было бы провести примерно по той же схеме, которая была использована выше для функции у = sin х. Но мы выберем путь, быстрее приводящий к цели. Сначала докажем две формулы , важные сами по себе (в этом вы убедитесь в старших классах), но пока имеющие для наших целей лишь вспомогательное значение.

Для любого значения t справедливы равенства

Доказательство . Пусть числу t соответствует точка М числовой n окружности, а числу * + - -точка Р (рис. 124; ради простоты мы взяли точку М в первой четверти). Дуги АМ и ВР равны, соответственно равны и прямоугольные треугольники ОКМ и ОЬР. Значит, О К = ОЬ, МК = РЬ. Из этих равенств и из расположения треугольников ОКМ и ОЬР в системе координат делаем два вывода:

1) ордината точки Р и по модулю и по знаку совпадает с абсциссой точки М; это значит, что

2) абсцисса точки Р по модулю равна ординате точки М, но отличается от нее знаком; это значит, что

Примерно так же проводятся соответствующие рассуждения в тех случаях, когда точка М принадлежит не первой четверти.
Воспользуемся формулой (это - формула, доказанная выше, только вместо переменной t мы используем переменную х). Что дает нам эта формула? Она позволяет утверждать, что функции

тождественны, значит, их графики совпадают.
Построим график функции Для этого перейдем к вспомогательной системе координат с началом в точке (пунктирная прямая проведена на рис. 125). Привяжем функцию у = sin х к новой системе координат - это и будет график функции (рис. 125), т.е. график функции у - соs х. Его, как и график функции у = sin х, называют синусоидой (что вполне естественно).

Свойства функции у = соs х.

у = соs х - четная функция.

Этапы построения отражены на рис. 126:

1) строим график функции у = соs х (точнее, одну полуволну);
2) растянув построенный график от оси х с коэффициентом 0,5, получим одну полуволну требуемого графика;
3) с помощью полученной полуволны строим весь график функции у = 0,5 соs х.

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.

Тема: Тригонометрические функции

Урок: Функция y=sinx, её основные свойства и график

При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.

Определим закон соответствия для .

Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).

Каждому значению аргумента ставится в соответствие единственное значение функции.

Из определения синуса вытекают очевидные свойства.

На рисунке видно, что т.к. это ордината точки единичной окружности.

Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент - это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.

Например, угол на единичной окружности соответствует точке на графике (рис. 2)

Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).

Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.

Рассмотрим свойства функции :

1) Область определения:

2) Область значений:

3) Функция нечетная:

4) Наименьший положительный период:

5) Координаты точек пересечения графика с осью абсцисс:

6) Координаты точки пересечения графика с осью ординат:

7) Промежутки, на которых функция принимает положительные значения:

8) Промежутки, на которых функция принимает отрицательные значения:

9) Промежутки возрастания:

10) Промежутки убывания:

11) Точки минимума:

12) Минимум функции:

13) Точки максимума:

14) Максимум функции:

Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.

А. Г. Мордковича. -М.: Мнемозина, 2007.

№№ 16.4, 16.5, 16.8.

Дополнительные веб-ресурсы

3. Образовательный портал для подготовки к экзаменам ().

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Функции у= sin x и y = cos x и их графики (сопровождающая презентация к уроку) КОРПУСОВА ТАТЬЯНА СЕРГЕЕВНА учитель математики МБОУ ЛСОШ № 2 им. Н.Ф.Струченкова Брянская обл.

ОПРЕДЕЛЕНИЕ Числовые функции, заданные формулами у= sin x и y = cos x , называют соответственно синусом и косинусом. 10.11.2013 КОРПУСОВА Т.С.

Функция y=sin x , график и свойства. 10.11.2013 КОРПУСОВА Т.С.

Синусоида у 1 - π/2 π 2 π 3 π х -3 π/2 - π 0 π/2 3 π/2 5 π/2 -1 10.11.2013 КОРПУСОВА Т.С.

у = sin(x+a) ПРИМЕР y 1 -1 π 2 π - π 10.11.2013 КОРПУСОВА Т.С.

у = sin x + a 1) y = sin x + 1 ; y 1 x - π 0 π 2 π x -1 x 2) y = sin x - 1 10.11.2013 КОРПУСОВА Т.С.

Построение графиков y=sin(x+m)+l y 1 - π 0 π 2 π 3 π x -1 10.11.2013 КОРПУСОВА Т.С.

Функция y = cos x , её свойства и график. 10.11.2013 КОРПУСОВА Т.С.

y = cos x у 1 - π/2 π 2 π 3 π х - π 0 π/2 3 π/2 5 π/2 -1 График функции у= cos x получен при смещении синусоиды влево на π/2 10.11.2013 КОРПУСОВА Т.С.

Построение графиков y = cos (x+m)+l 1)y =- cos x; y 2 y x 0 x -1 2)y= cos (x- π/4)+2 10.11.2013 КОРПУСОВА Т.С.

Построение графиков y=k · sin x y 2,5 1 x -1 -2,5 10.11.2013 КОРПУСОВА Т.С.

Нахождение периода тригонометрических функций Если y=f(x) периодическая и имеет наименьший положительный период Т₁, то функция y=A· f(kx+b), где А, k и b постоянные, а k ≠ 0 , также периодична с периодом Примеры: 10.11.2013 КОРПУСОВА Т.С. 1) y=sin 6 x +2, Т₁=2 π T₁=2 π

Построение графиков периодических функций 10.11.2013 КОРПУСОВА Т.С. y x 1 1 y x 1 1 1)T= 4 2)T= 4 Дана функция у= f(x) . Построить её график, если известен период. y x 1 1 3)T= 3

Построить график функции: y=2cos(2x- π/3)-0,5 и найти область определения и область значений функции 10.11.2013 КОРПУСОВА Т.С. у х 1 -1 π - π 2 π -2 π T= π

Мы выяснили, что поведение тригонометрических функций, и функции у = sin х в частности, на всей числовой прямой (или при всех значениях аргумента х ) полностью определяется ее поведением в интервале 0 < х < π / 2 .

Поэтому прежде всего мы построим график функции у = sin х именно в этом интервале.

Составим следующую таблицу значений нашей функции;

Отмечая соответствующие точки на плоскости координат и соединяя их плавной линией, мы получаем кривую, представленную на рисунке

Полученную кривую можно было бы построить и геометрически, не составляя таблицы значений функции у = sin х .

1.Первую четверть окружности радиуса 1 разделим на 8 равных частей.Ординаты точек деления окружности представляют собой синусы соответствующих углов.

2.Первая четверть окружности соответствует углам от 0 до π / 2 . Поэтому на оси х возьмем отрезок и разделим его на 8 равных частей.

3.Проведем прямые, параллельные оси х , а из точек деления восставим перпендикуляры до пересечения с горизонтальными прямыми.

4.Точки пересечения соединим плавной линией.

Теперь обратимся к интервалу π / 2 < х < π .
Каждое значение аргумента х из этого интервала можно представить в виде

x = π / 2 + φ

где 0 < φ < π / 2 . По формулам приведения

sin ( π / 2 + φ ) = соsφ = sin ( π / 2 - φ ).

Точки оси х с абциссами π / 2 + φ и π / 2 - φ симметричны друг другу относительно точки оси х с абсциссой π / 2 , и синусы в этих точках одинаковы. Это позволяет получить график функции у = sin х в интервале [ π / 2 , π ] путем простого симметричного отображения графика этой функции в интервале относительно прямой х = π / 2 .

Теперь, используя свойство нечетности функции у = sin х,

sin (- х ) = - sin х ,

легко построить график этой функции в интервале [- π , 0].

Функция у = sin х периодична с периодом 2π ;. Поэтому для построения всего графика этой функции достаточно кривую, изображенную на рисунке, продолжить влево и вправо периодически с периодом 2π .

Полученная в результате этого кривая называется синусоидой . Она и представляет собой график функции у = sin х.

Рисунок хорошо иллюстрирует все те свойства функции у = sin х , которые раньше были доказаны нами. Напомним эти свойства.

1) Функция у = sin х определена для всех значений х , так что областью ее определения является совокупность всех действительных чисел.

2) Функция у = sin х ограничена. Все значения, которые она принимает, заключены в интервале от -1 до 1, включая эти два числа. Следовательно, область изменения этой функции определяется неравенством -1< у < 1. При х = π / 2 + 2kπ функция принимает наибольшие значения, равные 1, а при х = - π / 2 + 2kπ - наименьшие значения, равные - 1.

3) Функция у = sin х является нечетной (синусоида симметрична относительно начала координат).

4) Функция у = sin х периодична с периодом 2π .

5) В интервалах 2nπ < x < π + 2nπ (n - любое целое число) она положительна, а в интервалах π + 2kπ < х < 2π + 2kπ (k - любое целое число) она отрицательна. При х = kπ функция обращается в нуль. Поэтому эти значения аргумента х (0; ±π ; ±2π ; ...) называются нулями функции у = sin x

6) В интервалах - π / 2 + 2nπ < х < π / 2 + 2nπ функция у = sin x монотонно возрастает, а в интервалах π / 2 + 2kπ < х < 3π / 2 + 2kπ она монотонно убывает.

Cледует особо обратить внимание на поведение функции у = sin x вблизи точки х = 0 .

Например, sin 0,012 ≈ 0,012; sin (-0,05) ≈ -0,05;

sin 2° = sin π 2 / 180 = sin π / 90 ≈ 0,03 ≈ 0,03.

Вместе с тем следует отметить, что при любых значениях х

| sin x | < | x | . (1)

Действительно, пусть радиус окружности, представленной на рисунке, равен 1,
a / AОВ = х .

Тогда sin x = АС. Но АС < АВ, а АВ, в свою очередь, меньше длины дуги АВ, на которую опирается угол х . Длина этой дуги равна, очевидно, х , так как радиус окружности равен 1. Итак, при 0 < х < π / 2

sin х < х.

Отсюда в силу нечетности функции у = sin x легко показать, что при - π / 2 < х < 0

| sin x | < | x | .

Наконец, при x = 0

| sin x | = | x |.

Таким образом, для | х | < π / 2 неравенство (1) доказано. На самом же деле это неравенство верно и при | x | > π / 2 в силу того, что | sin х | < 1, а π / 2 > 1

Упражнения

1.По графику функции у = sin x определить: a) sin 2; б) sin 4; в) sin (-3).

2.По графику функции у = sin x определить, какое число из интервала
[ - π / 2 , π / 2 ] имеет синус, равный: а) 0,6; б) -0,8.

3. По графику функции у = sin x определить, какие числа имеют синус,
равный 1 / 2 .

4. Найти приближенно (без использования таблиц): a) sin 1°; б) sin 0,03;
в) sin (-0,015); г) sin (-2°30").

Функция y = sin x

Графиком функции является синусоида.

Полную неповторяющуюся часть синусоиды называют волной синусоиды.

Половину волны синусоиды называют полуволной синусоиды (или аркой).

Свойства функции y = sin x :

3) Это нечетная функция. 4) Это непрерывная функция. - с осью абсцисс: (πn; 0), - с осью ординат: (0; 0). 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках функция принимает положительные значения. На промежутках [-π + 2πn; 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. Точки максимума функции: π/2 + 2πn наибольшее значение 1.

Для построения графика функции y = sin x удобно применять следующие масштабы:

На листе в клетку за единицу отрезка примем длину в две клетки.

На оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x .

На оси y отметим 1, включающий две клетки.

Составим таблицу значений функции, применяя наши значения x :

			√3 - 2		√3 - 2

Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке . Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].

Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.

Функция y = cos x .

Графиком функции является синусоида (ее иногда называют косинусоидой).

Свойства функции y = cos x :

1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: - с осью абсцисс: (π/2 + πn; 0), - с осью ординат: (0;1). 6) На отрезке функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. На промежутках [π/2 + 2πn; 3π/2 + 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. Промежутки убывания: ; 9) Точки минимума функции: π + 2πn. Точки максимума функции: 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π)

Функция y = mf (x ).

Возьмем предыдущую функцию y = cos x . Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.

Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.

Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.

Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.

Функция y = f (kx ).

Если функция y = mf (x ) приводит к растяжению синусоиды от оси x либо сжатию к оси x , то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y .

Причем k – любое действительное число.

При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.

Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.

Функция y = tg x .

Графиком функции y = tg x является тангенсоида.

Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.

Свойства функции y = tg x :

Функция y = ctg x

Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).

Свойства функции y = ctg x :